高考马上就到，很多考生都投入百分之两百的精力，期望在人生最重要一次考试中能取得好成绩。

今天我们就一起来讲讲高考数学考点对数函数问题。

我们知道，如果ax＝N(a>0且a≠1)，那么数x叫做以a为底N的对数，记作x＝logaN，其中a叫做对数的底数，N叫做真数．当a＝10时叫常用对数．记作x＝lg_N，当a＝e时叫自然对数，记作x＝ln_N。

对数函数的定义域及单调性：

在对数式中，真数必须大于0，所以对数函数y＝logax的定义域应为{x|x>0}．对数函数的单调性和a的值有关，因而，在研究对数函数的单调性时，要按0<a<1和a>1进行分类讨论．

典型例题1：

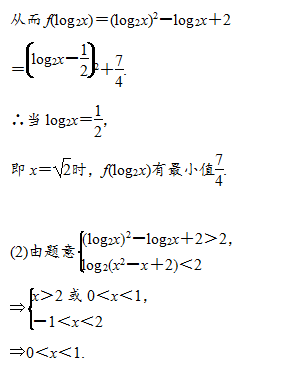
对数式的化简与求值的常用思路：

1、先利用幂的运算把底数或真数进行变形，化成分数指数幂的形式，使幂的底数最简，然后正用对数运算法则化简合并．

2、先将对数式化为同底数对数的和、差、倍数运算，然后逆用对数的运算法则，转化为同底对数真数的积、商、幂再运算．

我们把y＝logax(a>0，a≠1)叫做对数函数，其中x是自变量，函数的定义域是(0，＋∞)。函数y＝logax(a>0，a≠1)是指数函数y＝ax的反函数，函数y＝ax与y＝logax(a>0，a≠1)的图象关于y＝x对称．

研究复合函数y＝logaf(x)的单调性(最值)时，应先研究其定义域，分析复合的特点，结合函数u＝f(x)及y＝logau的单调性(最值)情况确定函数y＝logaf(x)的单调性(最值)(其中a>0，且a≠1)．

典型例题2：

对一些可通过平移、对称变换能作出其图象的对数型函数，在求解其单调性(单调区间)、值域(最值)、零点时，常利用数形结合求解。

一些对数型方程、不等式问题的求解，常转化为相应函数图象问题，利用数形结合法求解。

在运用性质logaMn＝nlogaM时，要特别注意条件，在无M>0的条件下应为logaMn＝nloga|M|(n∈N*，且n为偶数)．

对数值取正、负值的规律：

1、当a>1且b>1，或0<a<1且0<b<1时，logab>0；

2、 当a>1且0<b<1，或0<a<1且b>1时，logab<0.

我们还要记住下面这些性质：

一、对数的常用关系式(a，b，c，d均大于0且不等于1)：

1、loga1＝0.

2、logaa＝1.

3、对数恒等式：alogaN＝N.

4、换底公式：logab＝logcb/logca.

推广logab＝1/logba，logab·logbc·logcd＝logad.

二、对数的运算法则：

如果a>0，且a≠1，M >0，N>0，那么：

1、loga(M·N)＝logaM＋logaN；

2、logaNM＝logaM－logaN；

3、logaMn＝nlogaM(n∈R)；

4、log amMn＝n/mlogaM.